Abstract
Learning predictive models from observations using deep neural networks~(DNNs) is a promising new approach to many real-world planning and control problems. However, common DNNs are too unstructured for effective planning, and current control methods typically rely on extensive sampling or local gradient descent. In this paper, we propose a new framework for integrated model learning and predictive control that is amenable to efficient optimization algorithms. Specifically, we start with a ReLU neural model of the system dynamics and, with minimal losses in prediction accuracy, we gradually sparsify it by removing redundant neurons. This discrete sparsification process is approximated as a continuous problem, enabling an end-to-end optimization of both the model architecture and the weight parameters. The sparsified model is subsequently used by a mixed-integer predictive controller, which represents the neuron activations as binary variables and employs efficient branch-and-bound algorithms. Our framework is applicable to a wide variety of DNNs, from simple multilayer perceptrons to complex graph neural dynamics. It can efficiently handle tasks involving complicated contact dynamics, such as object pushing, compositional object sorting, and manipulation of deformable objects. Numerical and hardware experiments show that, despite the aggressive sparsification, our framework can deliver better closed-loop performance than existing state-of-the-art methods.
Video
Framework
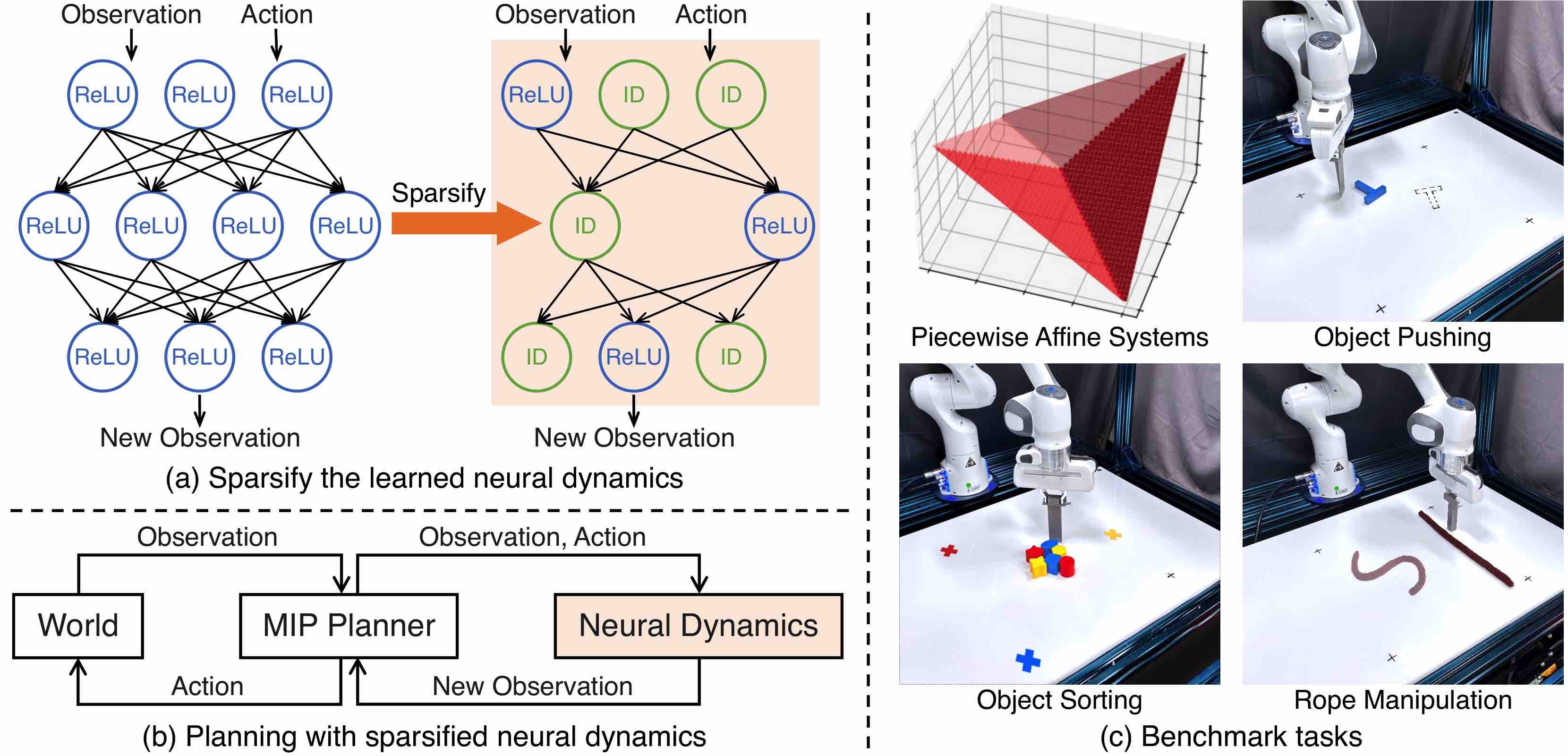
Model-based control with sparse neural dynamics. (a) Our framework sparsifies the neural dynamics models by either removing neurons or replacing ReLU activation functions with identity mappings (ID). (b) The sparsified models enable the use of efficient MIP methods for planning, which can achieve better closed-loop performance than sampling-based alternatives commonly used in model-based RL. (c) We evaluate our framework on various dynamical systems that involve complex contact dynamics, including tasks like object pushing and sorting, and manipulating a deformable rope.
Tasks
Piecewise Affine Function
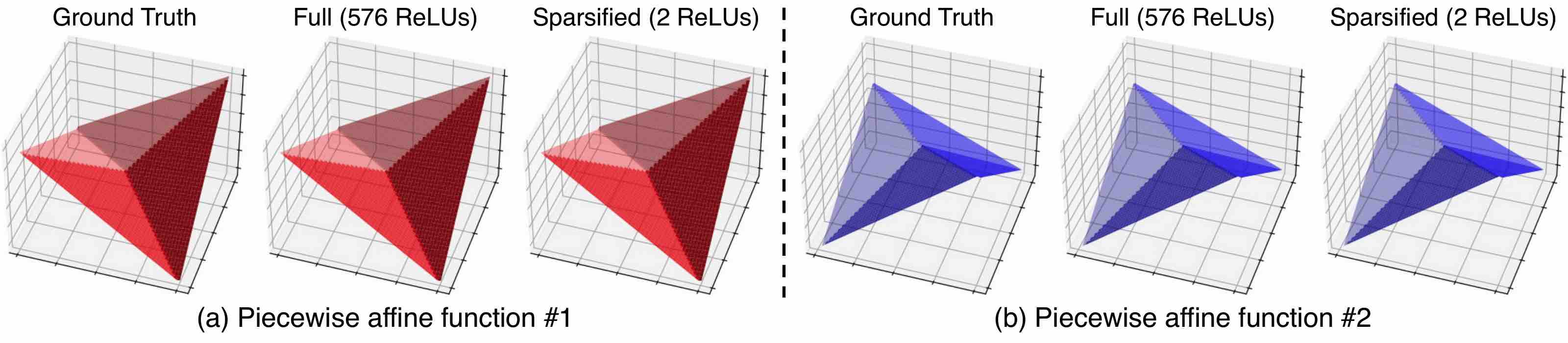
Recover the ground truth piecewise affine functions from data. We evaluate our sparsification pipeline on two hand-designed piecewise affine functions composed of four linear pieces. Our pipeline successfully generates sparsified models with 2 ReLUs that accurately fit the data, determine the region partition, and recover the underlying ground truth system.
Object Manipulation

Qualitative results on closed-loop feedback control. (a) In object pushing, the objective is to manipulate the object to reach a randomly generated target pose, depicted as transparent in the first column. The second column illustrates how the planner, using the sparsified model, can leverage feedback from the environment to compensate for the modeling errors and accurately achieve the target. (b) The framework is also applicable to rope manipulation. Our sparsified model, in conjunction with the MIP formulation, facilitates closed-loop feedback planning to manipulate the rope into desired configurations. (c) Our framework also consistently succeeds in object sorting tasks that involve complex contact events. Using the same model with the MIP formulation, the system can manipulate up to eight objects, sorting them into their respective regions.
Execution under Disturbances
BibTeX
@inproceedings{liu2023modelbased,
title = {Model-Based Control with Sparse Neural Dynamics},
author = {Liu, Ziang and Zhou, Genggeng and He, Jeff and Marcucci, Tobia and Fei-Fei, Li and Wu, Jiajun and Li, Yunzhu},
booktitle = {Thirty-seventh Conference on Neural Information Processing Systems},
year = {2023},
url = {https://openreview.net/forum?id=ymBG2xs9Zf}
}